ロボットアームをジェスチャーコントロールできたらいいのになぁ!アニメのように体のアクションでロボットコントロールできる?もしかしたら介護で使える?
介護の経験から、嚥下障害と手先が不自由になった母親に食事を食べさせるのは時間がかかり根気のいる介護です。自分も、もし、大変老後介護が必要となった時、自分で楽しみの食事ができるように!食べてる実感を感じられるように! ちょっとこんなんができればいいなぁ~との発想から考えてみました。ただいま試作中(^^♪
これは、ノートに記してはいますが、私の備忘録です。 皆さんにとってご参考になれば幸いです。(^^♪
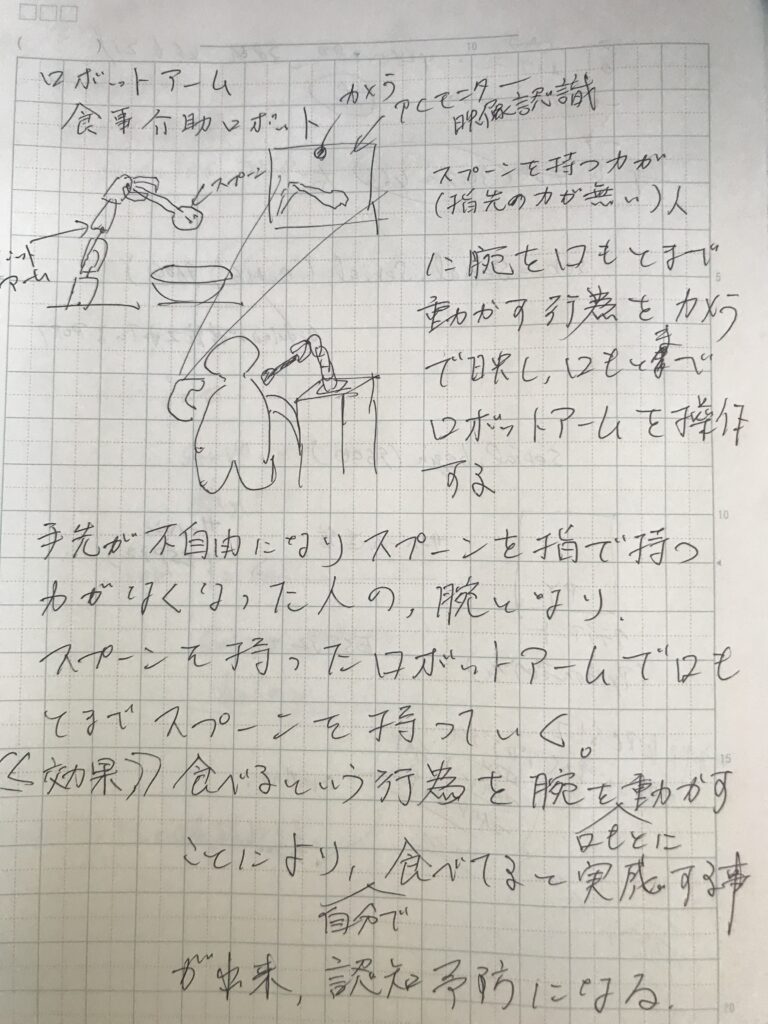
やり方としましては、VS CODEでpythonでMediapipeを実装し、シリアル通信でArduino IDEにシリアル値(角度)を送信し、サーボモーターを動かします。
まずは、Mediapipe poseのlandmark選定です。ここが、アームを動かすうえで重要だと思います。1つのパターンで1つのサーボモーターをうごかして、このパターンをほかのサーボモーター4つに適用して実装していきます。
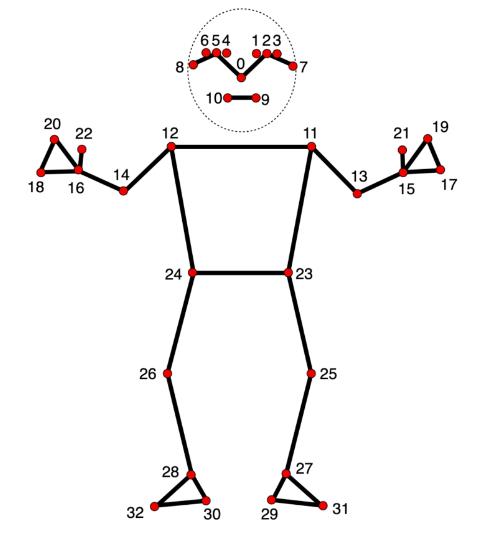
11,13,15のランドマークを使い角度を出していきます。どこの角度検出をするかで、アームのどのサーボモーターに当てはめるかは、少し迷いますが、まずは、この3点にしました。。
# ランドマーク15, 13, 11の間の角度を計算
lm_15 = landmarks[mp_pose.PoseLandmark.LEFT_WRIST.value]
lm_13 = landmarks[mp_pose.PoseLandmark.LEFT_ELBOW.value]
lm_11 = landmarks[mp_pose.PoseLandmark.LEFT_SHOULDER.value]
angle_15_13_11 = calculate_angle(lm_15.x, lm_15.y, lm_13.x, lm_13.y, lm_11.x, lm_11.y)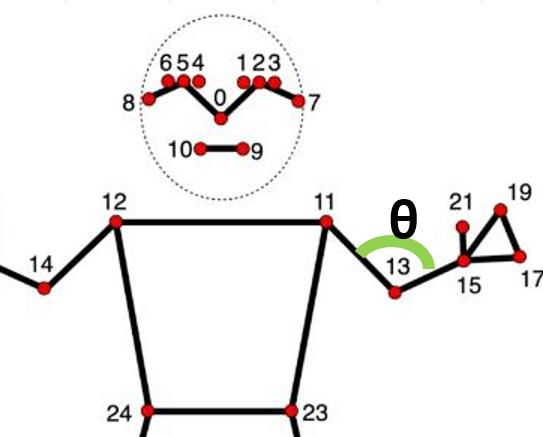
まず、各ランドマークでのサーボモーターの動きを確認します。
サーボ1の動作確認
サーボ2の動作確認
サーボ3の動作確認
サーボ4の動作確認
サーボ5の動作確認
部分部分ではまずまず動いてたのですが、連動になると、少々暴れてうまくいかなかったです。修正・調整が今後の課題です。
次回に続く~
いよいよプログラムに入ります。
import cv2
import mediapipe as mp
import time
import math
import serial
# シリアルポートの設定(Arduinoと接続されているポートを指定)
ser = serial.Serial('COM6', 9600) # ポート名は随時変更確認!
# Mediapipeの初期化
mp_pose = mp.solutions.pose
pose = mp_pose.Pose()
mp_drawing = mp.solutions.drawing_utils
# カメラのキャプチャ(パソコンの内蔵カメラ”0”)
cap = cv2.VideoCapture(0)
#map_value関数
def map_value(value, min_input, max_input, min_output, max_output):
# valueをmin_inputからmax_inputの範囲からmin_outputからmax_outputの範囲にマッピング
return min_output + (max_output - min_output) * ((value - min_input) / (max_input - min_input))
#角度計算
def calculate_angle(x1, y1, x2, y2, x3, y3):
# ベクトルABとBCを計算
vec_AB = (x2 - x1, y2 - y1)
vec_BC = (x3 - x2, y3 - y2)
# ベクトルの内積と大きさを計算
dot_product = vec_AB[0] * vec_BC[0] + vec_AB[1] * vec_BC[1]
magnitude_AB = math.sqrt(vec_AB[0]**2 + vec_AB[1]**2)
magnitude_BC = math.sqrt(vec_BC[0]**2 + vec_BC[1]**2)
# 角度を計算(アークコサイン)
angle_rad = math.acos(dot_product / (magnitude_AB * magnitude_BC))
angle_deg = math.degrees(angle_rad)
return angle_deg
while cap.isOpened():
success, image = cap.read()
if not success:
print("カメラからフレームを取得できませんでした")
break
# Mediapipe用に画像をRGBに変換
image_rgb = cv2.cvtColor(image, cv2.COLOR_BGR2RGB)
results = pose.process(image_rgb)
if results.pose_landmarks:
# ポーズランドマークを描画
mp_drawing.draw_landmarks(image, results.pose_landmarks, mp_pose.POSE_CONNECTIONS)
# ランドマークの位置を取得
landmarks = results.pose_landmarks.landmark
# ランドマーク15, 13, 11の間の角度を計算
lm_15 = landmarks[mp_pose.PoseLandmark.LEFT_WRIST.value]
lm_13 = landmarks[mp_pose.PoseLandmark.LEFT_ELBOW.value]
lm_11 = landmarks[mp_pose.PoseLandmark.LEFT_SHOULDER.value]
angle_15_13_11 = calculate_angle(lm_15.x, lm_15.y, lm_13.x, lm_13.y, lm_11.x, lm_11.y)
# 角度をサーボモーターの角度に変換(30度から130度の範囲にマッピング)
servo_angle = map_value(angle_15_13_11, 0, 180, 180, 20)
# Arduinoに角度を送信
ser.write(f"{int(servo_angle)}\n".encode())
# ランドマークと対応するサーボの角度を表示
cv2.putText(image, f'Servo: {int(servo_angle)}', (10, 30), cv2.FONT_HERSHEY_SIMPLEX, 1, (255, 0, 0), 2, cv2.LINE_AA)
# 画像を表示
cv2.imshow('Mediapipe Pose', image)
# 'q'キーで終了
if cv2.waitKey(5) & 0xFF == ord('q'):
break
cap.release()
cv2.destroyAllWindows()
ser.close()このプログラムの考え方ベクトル内積を説明していきます。
#角度計算
def calculate_angle(x1, y1, x2, y2, x3, y3):
# ベクトルABとBCを計算
vec_AB = (x2 - x1, y2 - y1)
vec_BC = (x3 - x2, y3 - y2)
# ベクトルの内積と大きさを計算 dot_productドット積は内積の意
dot_product = vec_AB[0] * vec_BC[0] + vec_AB[1] * vec_BC[1]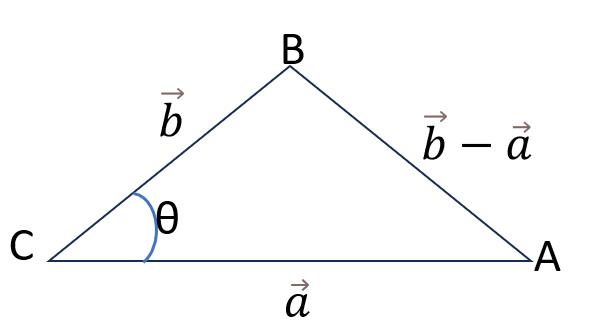
説明:ベクトル内積から角度を求める。(Mediapipe_landmark3点のなす角度)
![]() と
と![]() のなす角度を
のなす角度を![]() とする
とする![]() を
を![]() と
と![]() の内積と呼ぶ
の内積と呼ぶ
ベクトル内積は成分を用いると
![]() =(a1, a2),
=(a1, a2),![]() =(b1, b2) のとき
=(b1, b2) のとき
![]() ☚内積の公式
☚内積の公式
△CAB に余弦定理を適用すると
![]() 余弦定理
余弦定理
![]() ①
①
![]() なので
なので
![]()
ここでなぜ![]() になるかというと、
になるかというと、
ベクトル![]() の終点からベクトル
の終点からベクトル![]() の終点に向かうベクトルを考えると、
の終点に向かうベクトルを考えると、![]()
![]() の終点から
の終点から![]() の終点に向かう
の終点に向かう![]() とおくと、同じ始点からのつながりで考えると、
とおくと、同じ始点からのつながりで考えると、![]() となるので
となるので
ゆえに、![]() が分かる。ここで混乱してはならないことは、ベクトルは大きさだけでなく向きを持った量だということです。
が分かる。ここで混乱してはならないことは、ベクトルは大きさだけでなく向きを持った量だということです。
続けると
![]() とすると
とすると
![]()
両辺を整理すると
![]() =
=![]()
![]()
したがって、
![]()
より
![]()
わかりやすく簡単な例題で解いてみましょう(^^♪
![]() =(1,2)と
=(1,2)と![]() =(3,1)のなす角度を
=(3,1)のなす角度を![]() を求めるなら。。。。
を求めるなら。。。。
![]() ・
・![]() = 3+2 = 5
= 3+2 = 5
| ![]() |=
|= ![]() =
= ![]()
| ![]() |=
|= ![]() =
= ![]()
よって
![]() =
= ![]()
= ![]()
= ![]()
![]() = 45°
= 45°
簡単な例で解くとわかりやすいですね~
def calculate_angle(x1, y1, x2, y2, x3, y3):
# ベクトルABとBCを計算
vec_AB = (x2 - x1, y2 - y1)
vec_BC = (x3 - x2, y3 - y2)
# ベクトルの内積と大きさを計算
dot_product = vec_AB[0] * vec_BC[0] + vec_AB[1] * vec_BC[1]
magnitude_AB = math.sqrt(vec_AB[0]**2 + vec_AB[1]**2)
magnitude_BC = math.sqrt(vec_BC[0]**2 + vec_BC[1]**2)
ベクトルの大きさ(長さ)を計算しています。
ベクトルの大きさとは?
ベクトルの大きさとは、そのベクトルが持つ長さのことです。ベクトルを例に説明します。
ベクトルとは?
ベクトルは、方向と大きさを持つ量です。例えば、点Aから点Bへのベクトルを考えるとします。
ベクトルABのx成分 (vec_AB[0]):点Aのx座標から点Bのx座標を引いた値
ベクトルABのy成分 (vec_AB[1]):点Aのy座標から点Bのy座標を引いた値
大きさ(長さ)の計算方法
2次元のベクトルの大きさを計算するには、次のピタゴラスの定理を使います:
大きさ = ![]()
これは、直角三角形の斜辺を求めるのと同じです。これでベクトルの大きさを求めれます。
プログラムもいよいよ大詰めです。これは、ロボット工学の本で勉強しました。ロボットに三角関数は不可欠で、ロボットアームの位置を把握するものです。ここで出てくる、苦手だったアークコサイン・タンジェントの使い方が分かりました。
# 角度を計算(アークコサイン)
angle_rad = math.acos(dot_product / (magnitude_AB * magnitude_BC))
angle_deg = math.degrees(angle_rad)結論から言うと、math.acos()は引数として与えた数値の逆余弦(アークコサイン)をラジアン単位で返します。
2点でラジアンを出すのは、atan(アークタンジェント)で3点から角度を出すのは、ベクトル内積を使い、acos(アークコサイン)
を使います。acos(アークコサイン)について説明していきます。
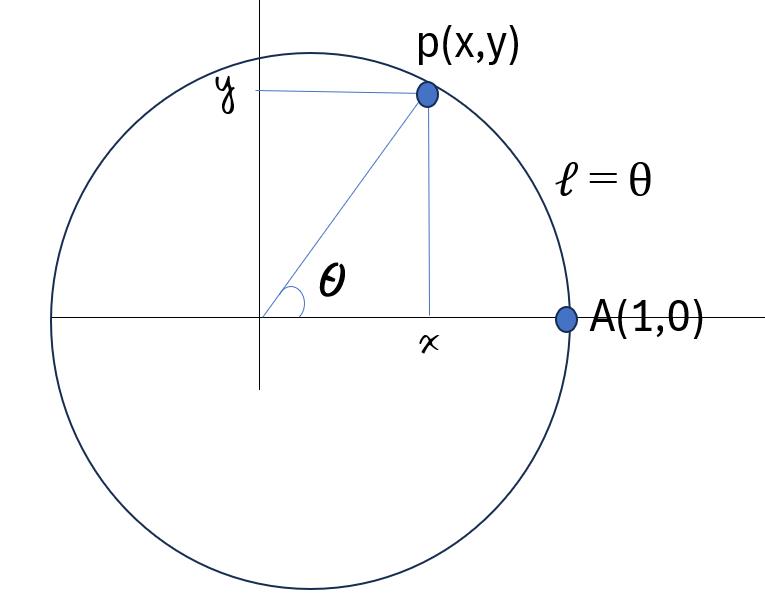
y=cosθのときθ=acos y です
acos y のyをcosθに置き換えると、θ=acos(cosθ)
そもそも角度を弧度法の単位であるラジアンで表すことは、角度θが見込む半径1の円上のアーク(弧)APの長さで表すということです。
例えばθ=360°であれば、単位円の全周だから半径r=1の円の円周は2πr=2πだからθ=2π(rad)である。
又、θ=60°であれば、アーク(弧)APの長さは、円周の1/6になるから、θ=2π/6=π/6(rad)になります。
![]() 角度θをラジアンであらわすと
角度θをラジアンであらわすと![]() 単位円上のアーク(弧)APの長さがθとなるような点P(x,y(x))のx座標を与える関数が
単位円上のアーク(弧)APの長さがθとなるような点P(x,y(x))のx座標を与える関数が
![]() である。
である。
![]() の逆関数が
の逆関数が![]() である。
である。
つまり単位円上の点A(1,0)からP(x,y(x))までのアーク(弧)APの長さθを与える関数は![]() である。
である。
そしてARCをつけて![]() =arcos x と表示します。
=arcos x と表示します。
angle_deg = math.degrees(angle_rad)アークコサインは角度で、そのコサインは数値になります。
返される角度は0(ゼロ)からPi(π)の範囲のラジアン単位になります。
結果をラジアンから角度に変換するには、結果を180/Pi(π)で乗算するかDgrees関数を使用します。
例えば
Acos(-0.5)は「2.0943951」
Acos(-0.5)*180/Pi は「120」を返します。
Dgrees(Acos(-0.5))は「120」になります。
次はArduinoでアーム(サーボモーター)を動かす。Arduino IDEでのコードです。
//************Arduino IDE*************
#include <Wire.h>
#include <Adafruit_PWMServoDriver.h>
// PCA9685の初期化
Adafruit_PWMServoDriver pwm = Adafruit_PWMServoDriver();
// サーボの最小・最大パルス幅
#define SERVOMIN 150 // パルス幅最小値
#define SERVOMAX 600 // パルス幅最大値
// サーボのチャンネル
#define SERVO_0_CHANNEL 0
void setup() {
Serial.begin(9600);
pwm.begin();
pwm.setPWMFreq(60); // サーボ周波数を60Hzに設定
delay(10);
}
void loop() {
if (Serial.available()) {
int angle = Serial.parseInt();
// サーボ角度をPWM信号に変換して設定
int pulse_0 = map(angle, 0, 180, SERVOMIN, SERVOMAX);
pwm.setPWM(SERVO_0_CHANNEL, 0, pulse_0);
}
}投稿
- 空撮事始め (2021年6月18日)
- 航空法施行規則改正されました。令和3年6月1日 (2021年6月19日)
- Tello(Ryze Technology 社 POWERED BY DJI)の飛ばし方マニュアル (2021年7月5日)
- 趣味におすすめ!ドローン(Tello)のいろいろな楽しさをお伝えします。 (2021年7月5日)
- プログラミング言語って?Pythonの導入前にプログラミング言語の種類をおおまかにまとめてみました。 (2021年7月6日)
- ドローンのプログラミングらしき事をやってみる! はじめてのPython&IDEのインストール方法 (2021年7月7日)
- Tello の画像をOpenCVでPCに写してみる!!OpenCVの導入方法 (2021年7月9日)
- これだけは知っておこう!ドローンを飛ばすのに法律って関係あるの? (2021年7月15日)
- ドローンの空撮は最高!きままに撮ってみました(^^♪ 空撮Gallery集 (2021年7月30日)
- ドローンを飛ばすなら これだけは知っておこう!ドローンの飛行ルール(令和3年6月施行) (2021年7月30日)
- これだけは知っておこう!ドローン空撮には注意が必要です。映像等のインターネット上での注意事項。 (2021年7月30日)
- OpenCVで遊んでみる。 PC内蔵webカメラから動画の撮影。 (2021年9月14日)
- PCでOpenCVで顔認識して遊んでみる。(^^♪ カスケード分類器の使い方 (2021年10月30日)
- ドローン・無人航空機の登録が義務化されます。リモートIDの付け方 (2021年12月14日)
- ドローンのプログラミングでOpenCVをつかい顔認識をしてみる (2022年1月9日)
- ドローン(Tello)を飛ばしてOpenCVで顔認識してみる改良版 (2022年2月21日)
- TelloでOpenCVで顔認識させたらFLIP(フリップ)させる(^^♪ (2022年5月2日)
- Pythonを使いTello(ドローン)でOpenCV(顔認識)から自動追尾をしてみる!☺ (2022年6月13日)
- フィンガーサインでドローン(Tello)を操縦してみた!MediaPipeを使用 (2022年9月29日)
- Pythonプログラミング・OpenCv&MediaPipeを使いドローン(Tello)を自由に操縦してみた! (2022年11月21日)
- Pythonで「Tello(ドローン)で自動追尾プログラミング」改良版を紹介します!これはいける! (2023年3月22日)
- OpenCVで遊んでみる。 PC内蔵カメラから映像の表示 と ドローンからの映像を表示をする (2023年4月13日)
- 100g未満のドローン、100g以上のドローンを飛ばすには?法律や準備しないといけないことは何? (2023年4月21日)
- mediapipe(メディアパイプ)& OpenCV・ Pythonでposeランドマーク検出Telloの自動操縦 (2023年5月8日)
- プログラミングで動かせるオススメ!ドローン・ロボット ベスト2選!! (2023年6月1日)
- 海外、子供に人気!プログランミングで動かせるドローンLitebeeWing紹介(パソコン接続方法解説)します。 (2023年7月2日)
- 講座用ダウンロード サイト (2023年7月7日)
- ドローン(Tello)を音声認識コントロールできる?パソコンで2か所Wi-Fi接続してGoogle Speech to Text (2023年7月9日)
- 最近はまっている 楽しーい気分転換アイテム ドローン&プログラミング学習用教材&ラジコン (2023年7月26日)
- Scratch(スクラッチ)ビデオモーションセンサーでTello(ドローン)操作 AR「拡張現実」? (2024年1月31日)
- スクラッチ(Scratch3-Tello) & (マイコンボード)micro:bitを使って、Telllo(ドローン)をコントロールしてみた(^^♪ (2024年5月5日)
- マイコンでドローン感知ロボットを作ってみました(^^♪ microbit & arduino (2024年6月1日)
- mediapipe & Arduino で 自称ロボットのジェスチャーコントロール (2024年6月5日)
- M5Stackを内蔵のESP32でWiFiサーバーとして使い、コードレスで無線ジェスチャーコントロールをしてみました(^^)/ (2024年6月12日)
- ロボットアームのジェスチャーコントロールへの挑戦 からだアクション操作*目指せ老後の食事介助アーム* (2024年6月27日)
- LiteBee Wing/ SKY / Tello でドローンプログラミングを教えます。プログラミングしたい人集まれ(^^♪ (2024年7月3日)
- 自由研究に!「ドローンをつくろう!学ぼう!」by 神戸ロボットクラブ (2024年8月17日)
- 加速度センサーとジャイロセンサーをArduinoで使って学び、Telloの慣性ユニットに触れる(^_-)-☆ (2025年1月16日)
- RobotDogを音声でコントロールする。音声認識によりコマンドを選定し、赤外線リモコン作り赤外線を送信し、ロボットをコントロールする。 (2025年2月5日)
- Tello ピンクのボールを追尾する(ピンク色のボール検出(OpenCV HSV)を使い追尾) (2025年6月1日)
- ソケット通信について・Telloとパソコンの交信を見てみよう! (2025年8月8日)
- ArUcoマーカーの検出を使った、Telloのプログラミングゲーム (2025年8月10日)
- 知りたかった、Telloの中身をのぞいてみた・これがTelloだ!! (2025年12月31日)
ダウンロード
- PCパソコンweb用 (2023年7月6日)
- ロボット写真 (2023年7月7日)
- 画像認識webcamera (2023年7月7日)
- 画像認識 顔 (2023年7月7日)
- 画像認識・ 目 (2023年7月7日)
- mediapipe finger (2023年7月7日)
- mediapipe pose (2023年7月7日)
- Tello DEMO Python (2023年7月7日)
- Tello SDK (2023年7月7日)
- 無題の動画-Made-with-Clipchamp (2023年7月26日)
- IMG_1966 (2023年7月26日)
- IMG_1959-1 (2023年7月26日)
- IMG_1960-2 (2023年7月26日)
- IMG_1964-1 (2023年7月26日)
- IMG_1960-1 (2023年7月26日)
- IMG_1964 (2023年7月26日)
- IMG_1960 (2023年7月26日)
- IMG_1959 (2023年7月26日)
- viwe (2023年7月26日)
- viwe (2023年7月26日)
- Telloカメラ (2024年2月29日)
タグ
- ドローン中身
- オシロスコープ
- NPO法人神戸ロボットクラブ
- 特定非営利活動法人神戸ロボットクラブ
- ドローンプログラミング
- python opencv
- ドローン自動追尾
- MPU6050
- ADLX345
- 加速度センサー
- ジャイロ
- 慣性ユニット
- IMU
- DSO152
- 自動追尾、
- 組立
- pyttsx3
- python
- diy
- Drone
- ソケット通信
- UDP通信
- ArUcoマーカー
- ゲーム
- ARマーカー
- ArUco
- Tello構造
- 自作ドローン
- 仕組み
- 小学生
- Scratch
- スクラッチ
- Otto
- 楽しい
- 知育教育
- 親子でプログラミング
- マッキーの趣味のドローン
- litebee
- litebeewing
- 自由研究
- ドローン
- 子供
- プログラミング 自動追尾
- モーションセンサー
- 教育
- マイコン、microbit
- arudino
- ロボット、レーダー、トイドローン
- プログラミング、顔認識、自動操縦
- プログラミング、自動操縦
- MediaPipe
- 神戸ロボットクラブ
- ロボット
- OpenCv
- プログラミング
- tello
- 食事介助、ロボットアーム、mediapipe
- プログラミング、大人の趣味、老後対策
- arduino


